프랙탈 구조와 주식 시장의 변동성 예측

프랙털 구조란

프랙탈(fractal)은 일부 작은 조각이 전체 구조와 비슷한 기하학적 형태를 말하고, 이러한 자기 유사성을 갖는 기하학적 구조를 프랙탈 구조라고 한다.

자연계에서 흔히 발견되는 프랙털 구조 중에서 대표적인 것은 눈송이이다. 눈송이를 자세히 들여다 보면 마치 나뭇가지와 같은 형상을 하고 있는 것을 볼 수 있다. 눈송이를 구성하는 가지를 다시 더 크게 확대해서 보면 역시 비슷한 가지가 나타난다.

이처럼 수는 많지만 크기가 작은 조각과 비슷하게 보이지만 크기가 다른 조각으로 이루어진 시스템을 프랙탈 구조라고 하고, 자기 복제에 의해 부분이 전체를 형성하는 것을 프랙털 시스템이라고 한다.

프랙털 시스템은 구름과 산, 해안선 및 나뭇가지에서도 관찰되고 번개와 난류에서도 프랙털 구조를 관찰할 수 있다. 즉, 부분과 전체가 같은 모양을 하고 있으면 프랙탈 시스템(fractal system)으로 볼 수 있다.

프랙털 기하학의 활용 분야

프랙털 기하학은 폴란드 태생 수학자 브누아 망델브로(1924 – 2010)¹가 처음 연구한 이래, 수학 분야의 하나로 자리 잡아 과학, 공학, 컴퓨터 예술 등 그 분야를 확장하고 있다. 현실 세계의 매우 불규칙한 물체들을 표현하기 위해서, 또 기술적으로 이미지 압축 등에서도 프랙탈 기하학이 사용되고 있다.

브누아 망델브로는 뉴톤 역학으로 설명할 수 없는 복잡한 자연 질서를 설명하는 이론인 프랙탈 기하학이 적용될 수 있는 대표적인 분야로 금융 시장을 꼽기도 했다.

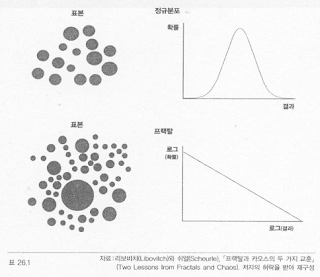
그는 <윌가에 적합한 복합 프랙탈 이론>에서 “포트폴리오 이론의 첫째 가정은 가격 변화가 통계적으로 서로 독립적이라는 것이다. 둘째 가정은 가격 변화의 분포가 정규 분포의 종(bell) 모양을 하고 있다는 것이다. 실제 시장 데이터들이 이런 가정을 만족하는가? 당연히 그렇지 않다.” 라고 단언했다.

금융 표준 이론에서는 자산 가격이 정규분포를 따른다고 가정한다. 이 가정은 대부분의 경우 대체로 정확하게 맞아서 분석을 할 때 표준의 평균과 평균에서 발생하는 편차를 간단히 구하는 확률 통계를 사용할 수 있도록 해 준다.

프랙털 기하학과 주식시장

하지만, 인간이 만든 주식시장을 포함해서 자연계의 많은 현상은 정규분포를 따르지 않는다는 데 문제점이 있다.

프랙털은 정규분포와 달리 적절하게 특정을 지울 수 있는 평균을 가지지 않는다. 프랙털 시스템은 오히려 파워 법칙²을 따른다. 프랙탈 시스템이 적용되는 금융 시장에 정규분포를 분석할 때 쓰는 통계 기법을 적용하여 예측하면 틀릴 수 밖에 없는 이유가 여기에 있다.

그런데도 수많은 시장의 이론가와 전망가들은 전통적인 통계 이론으로 매일 이런 일을 하며 뻘짓을 하고 있는 셈이다.

브누아 망델브로는 주가는 다수의 작은 변동 속에 커다란 변동이 군데 군데 뿌려져 있다고 한다. 이는 바로 정규 분포를 벗어나 극단에서 발생하는 뚱뚱한 꼬리, 블랙 스완을 말한다. 수 년에 한 번씩 발생하는 대폭락이나 대폭등이 수익률을 결정짓는다.

투자자들이 프랙탈 시스템에서 정규 분포를 벗어나는 뚱뚱한 꼬리가 언제 출현하는지 예의 주시해야 하는 까닭이다. 

금융 시장의 수익률은 정규분포 밖에서 결정되는 경우가 생각보다 훨씬 많이 일어난다. 최근 그 빈도가 더 잦아지는 느낌이다.

야구는 안타만 쳐도 경기에서 이길 수 있지만, 주식 시장에서는 큰 거 한방이 승부를 결정짓는다. 시장 수익률은 빈도보다는 사이즈가 결정적인 역할을 한다. 

그러니까 단타 보다는 장타가 주식 시장에서는 유리할 수 있다. 작게 작게 수익을 쌓아가다가 큰 거 한 방 맞고 쓰러지는 경우를 많이 보지 않았던가?

1. 브누아 망델브로는 1924년 폴란드 바르샤바 출생으로 제2차 세계대전 중 나치스의 박해를 받았다. 독창성이 뛰어 났으나 정규 교육을 제대로 이수하지는 못했다. 그는 혼돈 이론의 열쇠로 일컬어지는 프랙탈(fractal) 기하학의 창시자로 평가 받고 있다. ↩︎
2. 파워법칙(멱법칙, power law)은 한 수(數)가 다른 수의 거듭 제곱으로 표현되는 두 수의 함수적 관계를 의미한다. 예를 들면 2번째 큰 도시의 인구는 가장 큰 도시 인구의 대략 1/2이고 3번째 큰 도시의 인구는 가장 큰 도시 인구의 대략 1/3과 같더라는 법칙이다. 이는 전체 결과의 80%가 전체 원인의 20%에서 일어나는 현상을 가리키는 파레토 법칙(Pareto principle)과 유사하다. ↩︎
3. 『미래의 투자(MORE THAN YOU KNOW)』 마이클 모바신 저, 정명수 옮김, 위즈덤하우스, 2007년 ↩︎